Non-Abelian topological charge explains why certain Weyl points with different chirality do not annihilate upon collision
by Carey Sargent, NCCR MARVEL, EPFL
Robust properties of topological order such as protected edge states have opened up a route towards potentially translating mathematical understanding of physical phenomena into new quantum technology. This has in turn driven research into the topological band structures that can result in such physical features, and researchers have made considerable progress in cataloguing topological insulators and semimetals over the last decade. This brings us closer to being able to examine the potential of topological materials through experiment.
Notably, Weyl semimetals have been shown to exhibit topologically protected surface Fermi arcs and chiral-anomaly-induced negative magnetoresistance—Weyl semimetals in three-dimensional crystals give a paradigm example of topologically protected band nodes. Within this context, it is usually assumed that a pair of colliding Weyl points annihilate whenever they carry opposite chiral charge.
On the contrary, in the recently published paper, the scientists report that Weyl points in systems that are symmetric under the composition of time reversal with a π rotation are characterized by a non-Abelian topological invariant. The topological charges of the Weyl points are transformed through braid phase factors, which arise upon exchange inside symmetric planes of the reciprocal momentum space.
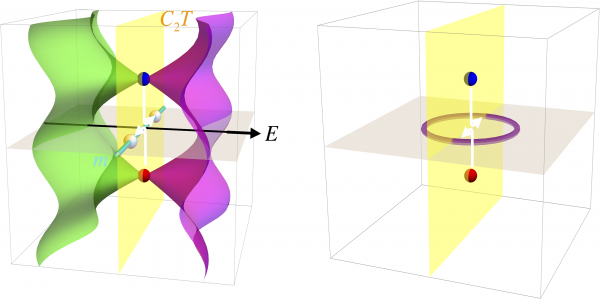
Conversion of Weyl points in 3D momentum space.
Specifically, Weyl points in three-dimensional systems with C2T symmetry carry non-Abelian topological charges, which are transformed via non-trivial phase factors that arise upon braiding the nodes inside reciprocal momentum space—the interplay of the non-Abelian topology with point-group symmetry enables topological phase transitions in which pairs of Weyl points may scatter or convert into nodal-line rings, greatly enriching the range of topological phase transitions for WPs in 3D crystals. This discovery adds to previous theoretical work on non-Abelian disclination defects in nematic liquids, Dirac lines in space–time-inversion symmetric metals and Dirac points of twisted bilayer graphene.
The researchers explain the reciprocal braiding process through a two-dimensional tight-binding model that can be put into place in both cold-atom set-ups and in photonic systems. They then consider three mathematically rigorous ways to characterize these phenomena and finally implement descriptions of the non-Abelian topology numerically via the Euler class. This reveals that it is the interplay of the non-Abelian charges with the chiralities of WPs and with mirror symmetry that leads to the non-trivial conversions between WPs and nodal lines.
Finally, they turned to first-principles modelling of the existing material zirconium telluride (ZrTe) and related compounds. These materials provide an ideal platform for studying the predicted conversions: the material class includes triple-point metals with a non-saturating quadratic magnetoresistance and, under ambient conditions, the band structure of ZrTe exhibits six pairs of WPs near the K point of BZ, all of them lying inside vertical C2T planes. The WPs are located only 50 meV above the Fermi level, which could be lowered even more by doping.
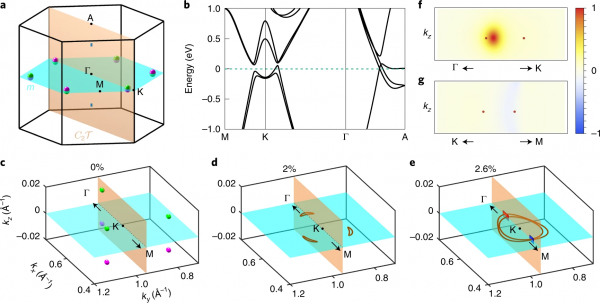
Figure 6 from paper
Performing high-precision first-principles computations, they found that a 2% compressive uniaxial strain in the z direction brings the pairs of WPs of ZrTe together at the m plane. Although experimentally challenging, the relatively low Young's modulus may allow for angle-resolved photoemission spectroscopy (ARPES) of ZrTe under large strains.
The relative mirror eigenvalues of the two bands forming the WPs are opposite, so the colliding WPs convert into NLs (brown lines, Fig. 6d). Further increasing the strain to 2.6% fuses three elongated NLs into two concentric NL rings (Fig. 6e). The reverse process of relaxing the strain of compressed ZrTe exhibits collisions of two NLs within the C2T Iplane along both the Γ-K and the K-M high-symmetry lines, though only the collisions along Γ-K eject pairs of WPs. They compared the two situations by computing the Euler class (3) inside the red and blue rectangular regions in Fig. 6e, each traversed by two NLs. The ejection of WPs from colliding NLs corresponds to a non-trivial Euler class on the rectangular region (Fig. 6f,g), consistent with their theoretical predictions.
The authors added that ZrTe is not the only such material that supports WPs with a non-trivial Euler class. First-principles calculations confirm that the Weyl semimetal TaAs and WC-type MoP and NbS also exhibit WPs under ambient conditions—the WPs of TaAs and MoP have even been observed with ARPES.
Reference: Bouhon, A., Wu, Q., Slager, R. et al. Non-Abelian reciprocal braiding of Weyl points and its manifestation in ZrTe. Nat. Phys. (2020). https://doi.org/10.1038/s41567-020-0967-9
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter