A new framework combines DFPT and algorithmic differentiation for improved materials modelling
By Nicola Nosengo/NCCR MARVEL
Predicting the properties of materials is at its core a mathematical problem. You start from the atoms that make up a material. You apply density functional theory (DFT) –a mathematical approximation of the laws of quantum mechanics - to calculate the electronic structure of the material at its lowest energy level. Then, if you want to predict how that material reacts to temperature changes or electrical charges, you compute derivatives of the DFT calculations. For those who need a math refresher, a derivative tells you how another function (the one from which it is derived) varies in response to changes in one of its variables.
Computing derivatives of DFT is the job of Density Functional Perturbation Theory (DFPT). While it is a well-established technique, and in principle a very accurate one, the manual derivation of all its necessary formulas for each new DFT variant is cumbersome and becomes a bottleneck. As a result, scientists often end up using other techniques that are easier to implement but are less accurate and require tweaking an extra parameter, such as finite differences methods.
In a new study in npj Computational Materials, scientists in Michael Herbst’s laboratory at EPFL – part of NCCR MARVEL – have combined DFPT with algorithmic differentiation (AD), a mathematical technique to compute derivatives of virtually any calculation codified in a computer program. The result is a new computational framework that makes DFPT easy by automatically deriving all necessary derivatives of DFT outputs for any input parameter, thus simplifying calculations of properties like elasticity of materials.
“Algorithmic differentiation is a set of techniques that compute exact derivatives of computer programs, from elementary subroutines with simple operations up to entire algorithms” says Niklas Schmitz, a doctoral student in Herbst’s lab and the first author of the article. “It has been used independently by different communities, from applied mathematics to machine learning”. In fact, a key to the success of neural networks is that one can take a library of components and build new networks out of them, and thanks to AD the gradients (the mathematical operators that tell you how the network parameters affect its errors) are computed automatically.
“We thought, what if we could apply the same concept to a first-principles model?” says Schmitz. Algorithmic Differentiation has already been applied to materials science problems – to find machine learning potentials, or to calculate derivatives of thermodynamic values in molecular dynamics. But it was never systematically integrated with DFT and DFPT, largely because AD is based on a very different mathematical language.
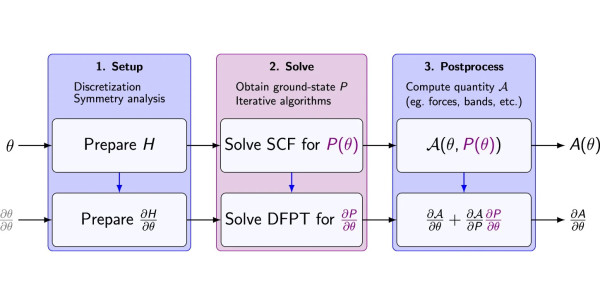
A representation of how plane-wave DFT is embedded into a general-purpose AD system, which across the entire simulation workflow A (top row) computes the end-to-end derivative (bottom row). From Schmitz et al. npj Comput Mater 12, 6 (2026).
The new AD-DFPT framework presented in the study allows a DFT code, the Density-functional toolkit (DFTK) created by Herbst’s lab, to interact seamlessly with a general-purpose AD system. Take as input a key parameter for a calculation, for example a specific geometry of the system. The workflow goes through a set-up stage that prepares the problem by applying discretization and symmetry analysis, a solution stage that determines a ground-state solution, and a postprocessing stage that yields the desired physical quantities such as total energy, forces, or band structure.
The team tested their workflow on some typical applications of DFPT, like the calculation of elastic constants, which characterize the linear response of a material to strain, to show that they are easily accessible in the new framework with minimal effort. The method also demonstrates potential for inverse materials design, where one starts from a desired set of properties and seeks atomic structures satisfying these properties most closely. When applied to tuning the band gap of the semiconductor gallium arsenide (GaAs) via strain engineering, AD-DFPT achieves the target band gap in just three iterations, avoiding the expensive grid searches often required by traditional methods. The effectiveness of the workflow was also tested on learning tasks, such as the learning of improved functionals or pseudopotentials for DFT. “The learning examples are particularly interesting”, says Schmitz “because they show that this technique could improve machine learning for materials science by allowing us to train DFT itself directly on the material properties we care about, instead of using only the total energy”.
Reference
Schmitz, N.F., Ploumhans, B. & Herbst, M.F. Algorithmic differentiation for plane-wave DFT: materials design, error control and learning model parameters. npj Comput Mater 12, 6 (2026). https://doi.org/10.1038/s41524-025-01880-3
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter