Automated, bespoke Wannier functions for all materials
By Nicola Nosengo, NCCR MARVEL
Wannier functions, first introduced by Swiss physicist Gregory Wannier in 1937, have been a foundational tool for theoretical condensed-matter physics ever since. Thanks to the introduction of maximally-localized Wannier functions by Marzari and Vanderbilt in 1997, and the algorithms and codes to calculate these in actual materials, they are nowadays a much used tool for computational condensed matter physics and materials science.
Wannier functions allow to represent the electronic structure of a solid as a set of chemically meaningful and intuitive localized orbitals that electrons can occupy – so in some ways allow to look at solids with the same concepts we use for molecules. This is very different from what theory teaches us, that electrons in a solid are delocalized, and should be represented as periodic states called Bloch states. As it often happens in physics, it’s just a matter of choosing the system of reference – we can describe the universe having the sun at its center, or the earth at its center, or anything else, and the math takes care of it all. Having a localized representation has key advantages when it comes to calculating or understanding many properties — from chemical bonding to polarization and magnetization, from conductivity to topological invariants — but until the 1997 work there were no general solutions to this task, and so Wannier functions saw little practical applications.
And even now, notwithstanding the thousands of papers published every year on the topic, obtaining Wannier functions for a given material (or, in the practitioners’ lingo, “Wannierizing” that material) requires as much art as science. The challenge is that of a magician – ones need to mix all the cards (the Bloch states) in the dark, and come out with something that is completely different. Scientists can guide this effort, “projecting” wavefunctions onto localized orbitals to make a transition from the extended representation to the localized one, and the way this projection is done can rely on chemical intuition, but often trial and error is needed until a satisfactory result is obtained.
Two newly-released articles by MARVEL members Junfeng Qiao, Giovanni Pizzi and Nicola Marzari provide instead now scientists with very robust and reliable algorithms that standardize and automatize the entire process. The twin papers have just been published (here and here) in npj Computational Materials. The reason for having two distinct publications is that the mathematical strategies involved in this two-step effort are very different. “The two articles seem to be solving the same problem, but behind the scenes they use very distinct concepts in differential geometry” says first author Junfeng Qiao. “For any material, we first want to obtain a good Wannier representation that is able to describe almost everything: all the occupied states, and the most relevant empty ones”. That means starting from atomic orbitals, identifying which states in the material have that character, and tracking and optimizing such character for every electron in the solid.
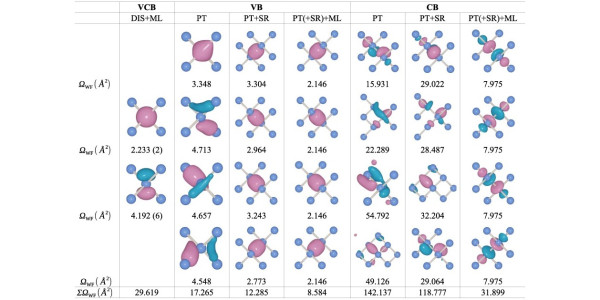
WF shape of various Wannierization methods. In the header, the left, center, and right columns correspond to the valence plus conduction bands (VCB), valence bands (VB), and conduction bands (CB), respectively. Full explanation in Figure 1 of Qiao, J., Pizzi, G. & Marzari, N. .npj Comput Mater 9, 206 (2023).
But that is not enough, Qiao explains. Take an insulator, where “two given atoms can form bonding orbitals, but you don’t really know how the bonding orbitals will look like, and often you can’t use your chemical intuition to guess it. So, we start from the step above, with the mathematical algorithm that mixes everything in first place. After that, another optimization algorithm can gradually remix these localized orbitals to make sure they only describe a target – e.g., only the occupied states of a material. This solves the chicken or the egg dilemma — people often use Wannier functions to understand chemical bondings in crystal, yet the conventional way of obtaining such Wannier functions relies on these chemical understandings, our approach removes the need of prior knowledge so that people can reliably analyze the chemistry”.
Previously, the crucial issue lied in that initial choice for the shape of the orbitals. “You are dealing with a very difficult optimization problem, with tens of thousands of variables that you are trying to optimize, so you need to choose the initial guess carefully to make the problem tractable. Many beginners who try to use existing codes are puzzled by the problem of how to do this, but we finally succeeded in automating the whole process” says Qiao.
To validate both algorithms, the scientists first chose four or five typical materials to explain how the methods work and reproduce what chemists would already guess about the materials. Then they stress-tested these algorithms on a larger set of materials to collect statistics and compare to previous approaches.
First, they picked graphene, silicon, copper, and strontium vanadate (SrVO3), and subsequently launched a mid-throughput study on a set of 200 structures. The results were compared with those from selected-columns-of-the-density-matrix (SCDM), a previous alternative that was tested in Marzari’s group years ago. “For metals, the new method is more effective at obtaining physically intuitive orbitals, whereas in the case of SCDM, the automated protocol for selecting input parameters could lead to Wannier functions resembling mathematical blobs that are difficult to understand from physics viewpoint,” Qiao explains. “And the new methods used less computer memory, which makes it more appealing for large scale or high-throughput calculations”. The new algorithm proved both more accurate and more economical – something the authors demonstrated by calculating over 1.3 million Wannier functions from 21,000 materials from the Materials Cloud MC3D database of bulk crystals.
On top of this, the second paper showed how one can take these Wannier building blocks, and mix them with each other aiming to reproduce only well-defined energy ranges, such as the occupied valence bands of a semiconductor, or the flat bands at the Fermi energy of a correlated metal. The first round of validation was done on silicon, a 2D MoS2 monolayer, and again SrVO3, that is a metallic perovskite, followed by a wider test on 77 insulators. While SCDM was already working quite well for the occupied bands of these materials, the main advantage seen here lies in its ability to obtain simultaneously Wannier functions for both occupied and empty bands, and the reduced use of computing resources. The validation study showed that the algorithm can robustly reproduce the way chemists understand the insulators on the list, and that could be applied to study properties such as electric polarization, electronic band gaps, and theories for correlated electrons.
References
Qiao, J., Pizzi, G. & Marzari, N. Projectability disentanglement for accurate and automated electronic-structure Hamiltonians. npj Comput Mater 9, 208 (2023). https://doi.org/10.1038/s41524-023-01146-w
Qiao, J., Pizzi, G. & Marzari, N. Automated mixing of maximally localized Wannier functions into target manifolds. npj Comput Mater 9, 206 (2023). https://doi.org/10.1038/s41524-023-01147-9
Low-volume newsletters, targeted to the scientific and industrial communities.
Subscribe to our newsletter